Inference-time scaling for diffusion models beyond scaling denoising steps
Methodology
We formulate the challenge as a search problem over the sampling noises; in particular, how do we know which sampling noises are good, and how do we search for such noises?
All experiments are conducted on ImageNet for class-conditional generation.
How to Scale at Inference Time
On a high-level, there are two design axes we propose to consider:
-
Verifiers are used to evaluate the goodness of candidates. These typically are some pre-trained models that are capable of providing feedback; concretely, verifiers are functions
\[\mathcal{V} : \mathbb{R}^{H \times W \times C} \times \mathbb{R}^d \rightarrow \mathbb{R} \tag{1}\]that takes in the generated samples and optionally the corresponding conditions, and outputs a scalar value as the score for each generated sample.
-
Algorithms are used to find better candidates based on the verifiers scores. Formally defined, algorithms are functions \(f : \mathcal{V} \times D_\theta \times \left\{ \mathbb{R}^{H \times W \times C} \times \mathbb{R}^d \right\}^N \rightarrow \mathbb{R}^{H \times W \times C} \tag{2}\) that takes a verifier $\mathcal{V}$, a pre-trained Diffusion Model $D_\theta$, and $N$ pairs of generated samples and corresponding conditions, and outputs the best initial noises according to the deterministic mapping between noises and samples. Throughout this search procedure, $f$ typically performs multiple forward passes through $D_\theta$. We refer to these additional forward passes as the search cost, which we measure in terms of NFEs as well.
Proof of Concept
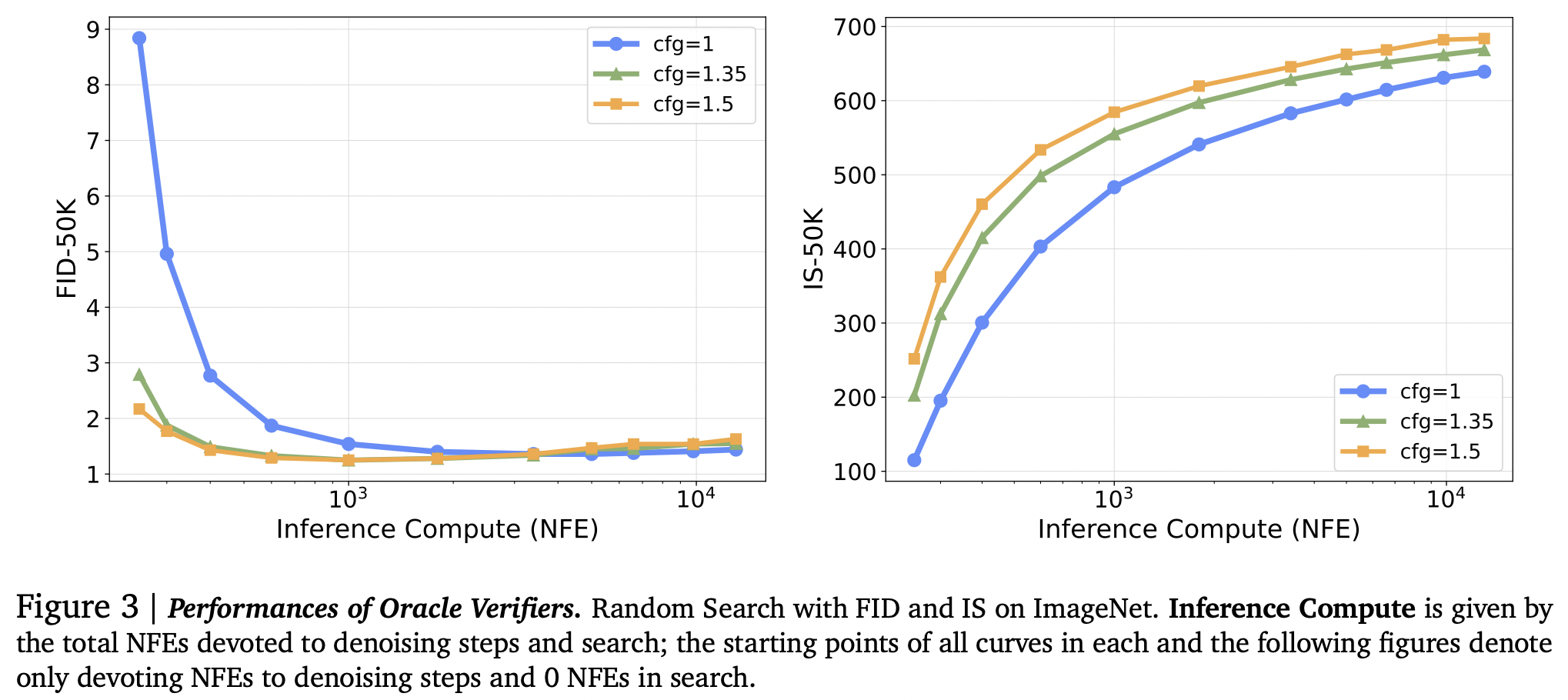
As a proof of concept, the authors employ a random search strategy over multiple generated samples for the same condition, utilizing ODE generation and refining the result metric, such as FID and IS, using greedy search.
Supervised Verifier for conditioning
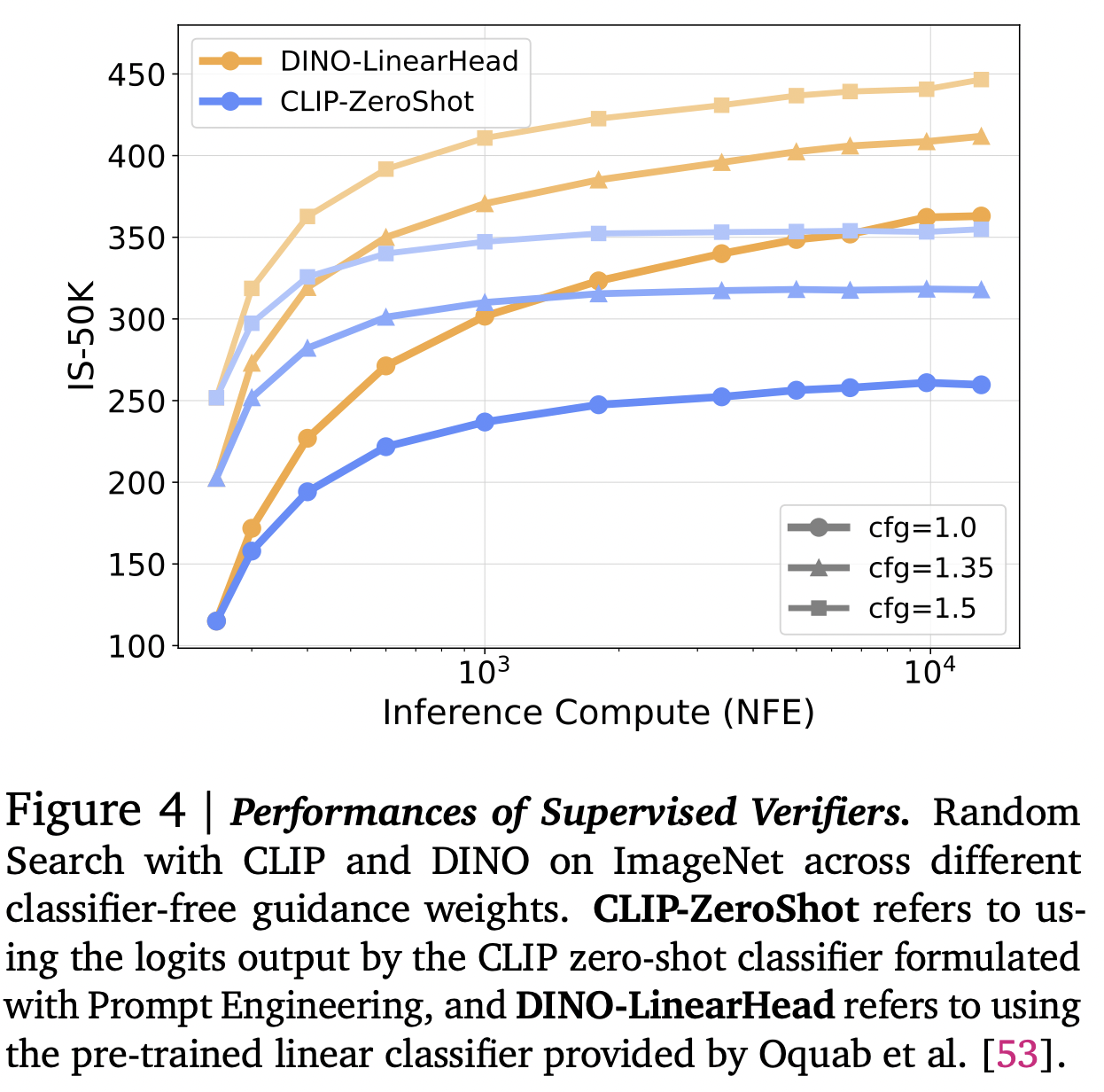
While scaling NFEs with search demonstrates impressive performance with the oracle verifiers, the key question is whether its effectiveness can be generalized to supervised verifiers with more accessible pre-trained models designed for various vision tasks.
The authors focus on improving conditioning in this section. They utilize two classifiers, CLIP and DINO, selecting samples based on the highest predicted probability.
This strategy also effectively improves the model performance on IS. Nevertheless, we note that, as these classifiers operate point-wise, they are only partially aligned with the goal of FID score. Specifically, the logits they produce only focus on the quality of a single sample without taking population diversity into consideration, which leads to a significant reduction in sample variance and eventually manifests as mode collapse as the compute increases. We term it as \(\textit{Verifier Hacking}\).
Self-Supervised Verifiers
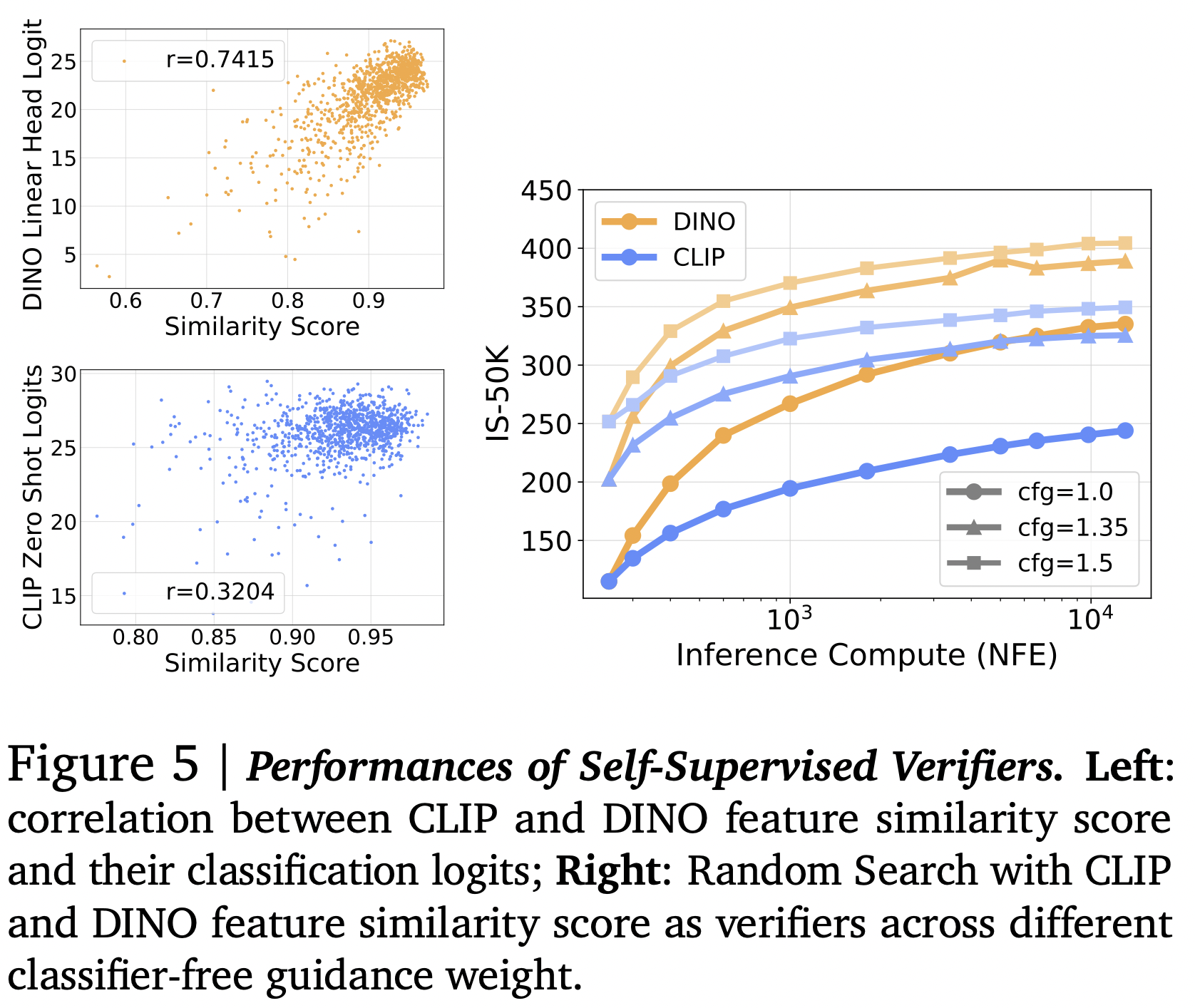
The authors observed that the logit prediction of the classifier is correlated with the similarity between the x-predictions of the diffusion model at different stages of generation ($\sigma = 0.4$ and $\sigma = 0$).
This result is encouraging for use cases where conditioning information is not available or hard to obtain.
Zero-Order Search (ZO-n)
Previous explorations have predominantly considered a simple random search setup, which is a one-time best-of-N selection strategy on a randomly chosen fixed set of candidates. To mitigate overfitting risks the author propose Zero-Order Search approach:
- We start with a random Gaussian noise $\mathbf{n}$ as pivot.
- Find $N$ candidates in the pivot’s neighborhood. Formally, the neighborhood is defined as $S_n^\lambda = { \mathbf{y} : d(\mathbf{y}, \mathbf{n}) = \lambda }$, where $d(\cdot, \cdot)$ is some distance metric.
- Run candidates through an ODE solver to obtain samples and their corresponding verifier scores.
- Find the best candidates, update it to be the pivot, and repeat steps 1–3.

Search over Paths (Paths-n)
- Sample $N$ initial i.i.d. noises and run the ODE solver until some noise level $\sigma$. The noisy samples $x_\sigma$ serve as the search starting point.
- Sample $M$ i.i.d. noises for each noisy sample, and simulate the forward noising process from $\sigma$ to $\sigma + \Delta f$ to produce ${ x_{\sigma + \Delta f} }$ with size $M$.
- Run ODE solver on each $x_{\sigma + \Delta f}$ to noise level $\sigma + \Delta f - \Delta b$, and obtain $x_{\sigma + \Delta f - \Delta b}$. Run verifiers on these samples and keep the top $N$ candidates. Repeat steps 2–3 until the ODE solver reaches $\sigma = 0$.
- Run the remaining $N$ samples through random search and keep the best one.
Since the verifiers are typically not adapted to noisy input, we perform one additional denoising step in step 3 and use the clean x-prediction to interact with the verifiers.
Inference-Time Scaling in Text-to-Image
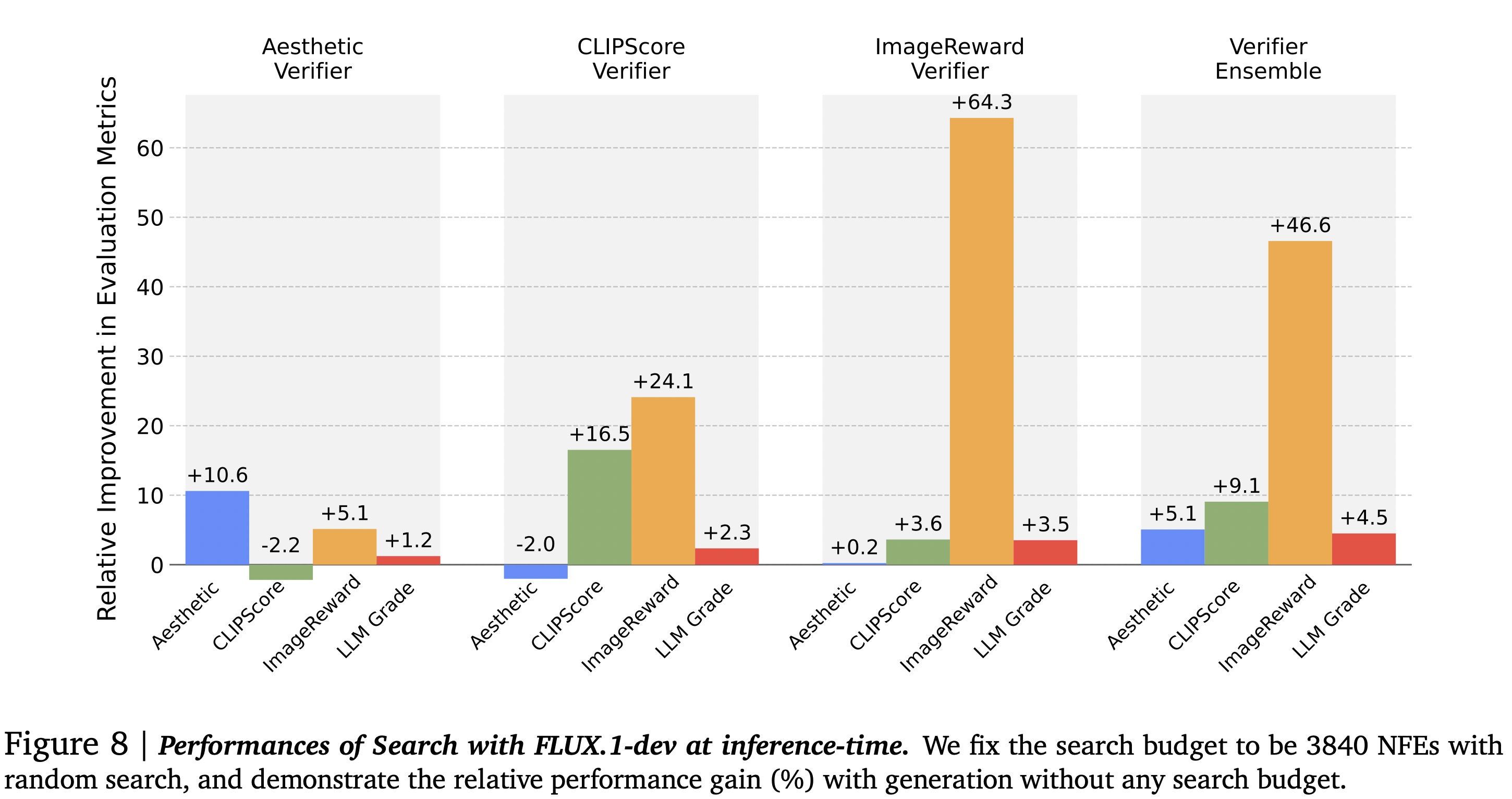
In this setup, the authors employ random search on the DrawBench benchmark using various models (indicated at the top of each graph). They then examine how this impacts validation across all models compared to generation without search (represented by vertical bars).
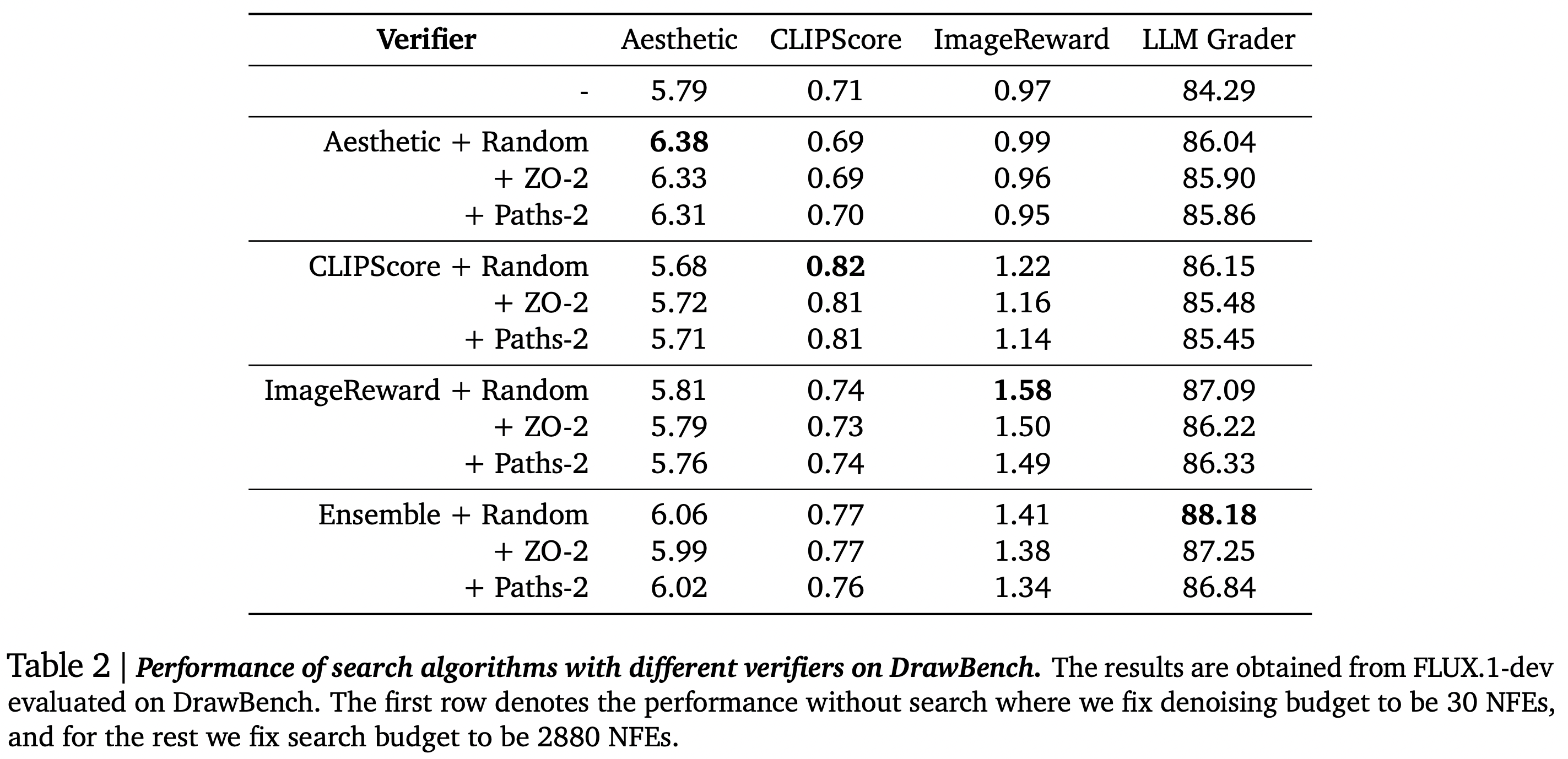
The authors then apply algorithms developed for class-conditional generation tasks. It is evident that the results do not transfer well to more complex tasks.